|
|
||
|
|
|
|
Les composantes symétriques permettent surtout d?étudier le fonctionnement d?un réseau polyphasé de constitution symétrique lorsque l?on branche en un de ses points un récepteur déséquilibré. Soit parce qu?il s?agit effectivement d?une charge non équilibrée soit plus fréquemment lorsque se produit un court circuit.
Condition d?emploi des composantes symétriques :
L?utilisation des composantes symétriques à un système récepteur/générateur exige que l?on puisse pratiquer le principe de superposition, c'est à dire que les relations doivent être linéaires (R=cte, L=Cte ) ce qui signifie absence de saturation et de distorsion.
Pour étudier dans ces
conditions le fonctionnement d?un réseau soumis à un système
de courants déséquilibrés, il suffit de connaître
son comportement devant chacun des systèmes composants pris isolement.
A l?attention des lecteurs :
Une bonne connaissance du
calcul matriciel ainsi que la maîtrise des nombres complexes facilitent
grandement la lecture de ce cours.
Convention d?écriture :
![]() sera noté V1,2,3 de même
sera noté V1,2,3 de même ![]() sera noté Vo,d,i
sera noté Vo,d,i
I Principe
La méthode des composantes symétriques consiste à substituer à un système initial déséquilibré de " q " grandeurs complexes quelconque un système de " q " grandeurs génératrices, permettant de définir " q " systèmes symétriques.
La transformation est assurée
par un opérateur matriciel complexe appelé matrice de Fortescue
noté [Fq], dont les coefficients sont formés à partir
de la résolution l?équation complexe ![]() .
.
Cette équation peut s?écrire :


II Application au système triphasé
Rappel
Dans le cas d?un système
triphasé direct.
 |
En
prenant le vecteur V1 comme origine il vient alors.
Dans un système équilibré direct
|
Soit un système triphasé ( q=3) déséquilibré de grandeurs sinusoïdales, de tensions simples V1, V2, V3. On peut donc considérer ce système déséquilibré comme la superposition de 3 systèmes équilibrés :
Un système de 3 grandeurs complexes V1,V2,V3 se décompose en 3 systèmes symétriques.
- Un système homopolaire (défini par Vo) constitué de 3 grandeurs ayant le même module le même argument.
![]()
Les vecteurs Vo, Vd et Vi sont appelés composantes ou coordonnées symétriques du système de vecteurs V1,V2,V3.
Les coefficients de la matrice
de Fortescue sont alors formées par la résolution de l?équation ![]() .
.
On a alors : ![]()
D?où  avec
avec 
On définit la matrice
de Fortescue F3 ainsi  et son inverse
et son inverse 
Il suffira alors de multiplier par F3 les composantes réelles du système triphasé pour obtenir les composantes symétriques et de multiplier les composantes symétriques par F3-1 pour revenir au système réel.
|
|
|
 |
 |
 |
 |
Représentation graphique de la transformation de Fortescue et de son inverse, sur un système de courants triphasés.

III Schéma équivalent
Pour utiliser les composantes on résonne sur le schéma équivalent monophasé, correspondant aux 3 systèmes (Homopolaire, direct, inverse) du générateur triphasé supposé également symétrique.
Chaque phase est caractérisée par son impédance propre Z et par les impédance mutuelles Z?, Z?? relative respectivement à la phase précédente et à la phase suivante.

Le système générateur
peut s?écrire alors :
 |
Ou bien matriciellement |  |
D?après les conventions
adoptées au début nous écrirons par la suite:
 |
Nous
avons démontré au chapitre précédent que :
|
que l?on note ![]() de la même manière on peut donc écrire
de la même manière on peut donc écrire ![]()
D?où

|
|
 |
 |
|
 |
 |
 |
|
IV Conduite des calculs
Enfin après toute cette mise au point nous allons aborder la partie la plus intéressante des composantes symétriques, le calcul de courant de court circuit.
 |
 Avec
Zog,Zdg,Zig impédances symétriques du générateur
et Zoc,Zdc,Zic impédances symétriques de la charge. Avec
Zog,Zdg,Zig impédances symétriques du générateur
et Zoc,Zdc,Zic impédances symétriques de la charge. |
| Aux bornes de la charge nous pouvons écrire : |
 |
|
|
|
 |
|
 |
|
 |
|
V Application
Une ligne triphasée est alimentée par un transformateur dont le secondaire est monté en étoile avec le neutre relié à la terre. Le système de tensions fourni par le transformateur est un réseau symétrique direct.
![]()
La tension simple entre phase et neutre est 220V. Les impédances directe, inverse et homopolaire de l?ensemble ligne + transformateur ont pour valeur :
![]()
Ce dispositif alimente un récepteur triphasé monté en étoile ayant pour chaque phase les impédance suivantes :
![]()
Calculs des impédances homopolaire, directe et inverse du récepteur.
| D?après l?énoncé on a Z?=Z?? et comme |
 |
| on
a alors
|
 |
Calculs des courants de lignes .
| Le système étant directe et sans défaut on utilise les relations ci-contre |
 |
| L?absence de défaut entraîne qu?il n?existe pas de courant homopolaire et inverse. |
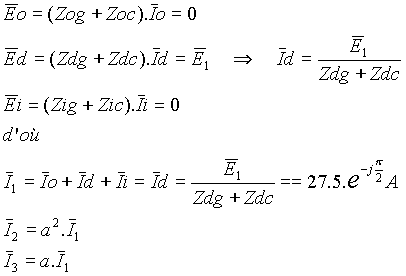 |
Calculs des tensions simples.
| Aux bornes de la charge on a : |
 |
D?où  |
 |
Voilà pour le système
lorsqu?il est équilibré. Maintenant que vous êtes chaud
passons à l?étude du même système mais cette
fois on ajoute une charge d?impédance ![]() entre la phase 1 et la terre.
entre la phase 1 et la terre.
Calculs des nouvelles tensions simples
| L?apparition de Z1 entraîne que le système n?est plus équilibré. On va donc utiliser les relations ci-contre |
 |
| Ce qui donne puisque toutes les impédances sont connues : |
 |
| D?autre
part
|
|
| Calcul de V1c |
 |
| Calcul de V2c |
 |
| Calcul de V3c |
 |
Calculs des nouveaux courants de lignes
| En se référant aux schémas équivalent lors d?un défaut on a : |
 |
| Calcul de Io |
 |
| Calcul de Id |
|
| Calcul de Ii |
 |
| Il ne reste plus qu?a appliquer la transformation de Fortescue. |
 |
 |